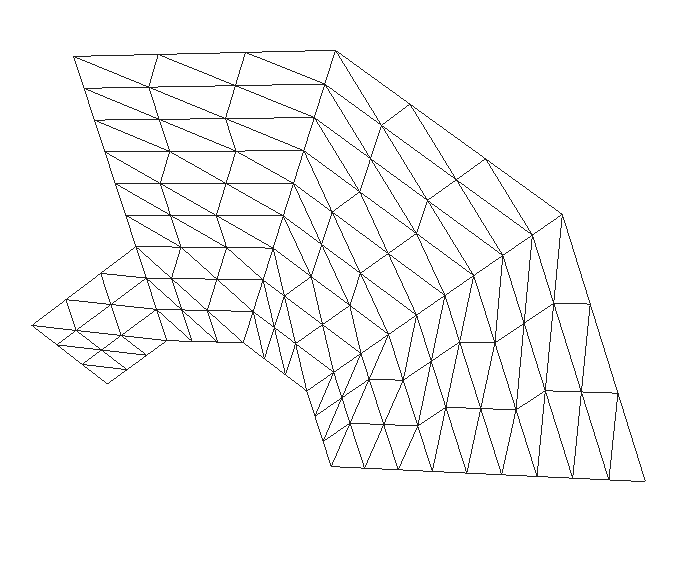
Здравствуйте, имеется триангуляция поверхности, заданной алгоритмом измельчения, выводящее изображение в stl файл. Как можно данную поверхность ограничить системой неравенств? Я знаю, что система неравенств в виде кода задается при помощи такого фрагмента кода:
Z[i] = 0.3 * (pow(X[i], 2) + pow(Y[i], 2)) && abs(X[i])-abs(Y[i])<4 && pow(X[i],2)+pow(Y[i],2)>1;
Как эту фрагментацию кода можно отобразить в программе, где просто задается триангуляция поверхности, заданная алгоритмом измельчения?
#include <iostream>
#include <algorithm>
#include <fstream>
#include <math.h>
#include <functional>
#define pi 3.14159265358979323846
using namespace std;
struct Point {
double x, y;
};
int a = 0;
double b = 2*pi;
int n = 10;
int m = 3;
int Q = 4;
int savetostl(double* XX, double* YY, int** T, int size_T);//для сохранения триангуляции в формате STL
int savetostl(double* XX, double* YY, int** T,int size_T)
{
int k = 0, ia, ib, ic;
fstream TRstl;
TRstl.open("triangulation.stl", ios::out | ios::app);
TRstl.close();
TRstl.open("triangulation.stl", ios::out | ios::in);
TRstl << "solid <Triangulation>\n";
for (k = 0; k < size_T; k++)
{
ia = T[k][0];
ib = T[k][1];
ic = T[k][2];
TRstl << "facet normal " << 0.0 << " " << 0.0 << " " << 1.0 << "\n";
TRstl << "outer loop\n";
TRstl << "vertex ";
TRstl << XX[ia] << " " << YY[ia] << " " << 0.0 << "\n";
TRstl << "vertex ";
TRstl << XX[ib] << " " << YY[ib] << " " << 0.0 << "\n";
TRstl << "vertex ";
TRstl << XX[ic] << " " << YY[ic] << " " << 0.0 << "\n";
TRstl << "endloop\n";
TRstl << "endfacet\n";
}
TRstl << "endsolid";
TRstl.close();
return 0;
}
double F(double O) {
return 3;
}
double Y(double O) {
return 10;
}
double Gr(double O, double r) {
return r * Y(O) + (1 - r) * F(O);
}
void Not_borderline(int**& T,int size_T,double*& X,double* &Y,int q ) {
int sizeT = size_T * q * q;
int** newT = new int*[sizeT];
for (int i = 0; i < sizeT; i++) {
newT[i] = new int[3];
}
double* NewX = new double[size_T * ((q+2) * (q+1)/2)];
double* NewY = new double[size_T * ((q+2) * (q+1)/2)];
int numbDot = 0;
int numbRect = 0;
double* ACDX = new double[q - 1]; //точки на прямой АС
double* ACDY = new double[q - 1];
double* ABDX = new double[q - 1]; // на прямой AB
double* ABDY = new double[q - 1];
double* internal_points_X = new double[(q - 1) * q / 2];
double* internal_points_Y = new double[(q - 1) * q / 2];
for (int i = 0; i < size_T; i++) //главный цикл обраотки всех треугольников
{
Point a, b, c;
a.x = X[T[i][0]];
a.y = Y[T[i][0]];
b.x = X[T[i][1]];
b.y = Y[T[i][1]];
c.x = X[T[i][2]];
c.y = Y[T[i][2]];
Point vectorAC;
vectorAC.x = c.x - a.x;
vectorAC.y = c.y - a.y;//напр вектор АС
Point vectorAB;
vectorAB.x = b.x - a.x;
vectorAB.y = b.y - a.y;//напр вектор BС
for (int i = 0; i < q - 1; i++) {
ACDX[i] = ((i + 1) * vectorAC.x / q) + a.x;
}
for (int i = 0; i < q - 1; i++) {
ACDY[i] = ((i + 1) * vectorAC.y / q) + a.y;
}
for (int i = 0; i < q - 1; i++) {
ABDX[i] = ((i + 1) * vectorAB.x / q) + a.x;
}
for (int i = 0; i < q - 1; i++) {
ABDY[i] = ((i + 1) * vectorAB.y / q) + a.y;
}//заполняем массивы точками лежащими на прямых ас и бс
int k = 0;
Point vectorABDACD;
for (int i = 1; i < q; i++) {
if (i != q - 1) {
vectorABDACD.x = ACDX[i] - ABDX[i];
vectorABDACD.y = ACDY[i] - ABDY[i];//вектор прямой между точками на AB и AC
}
else {
vectorABDACD.x = c.x-b.x;
vectorABDACD.y = c.y - b.y;
}
for (int j = 0; j < i; j++) {
if (i != q - 1) {
internal_points_X[k] = ABDX[i] + (j+1)*vectorABDACD.x/(i+1);
internal_points_Y[k] = ABDY[i] + (j + 1)* vectorABDACD.y / (i + 1);
}
else {
internal_points_X[k] = b.x + (j + 1) * vectorABDACD.x / (i + 1);
internal_points_Y[k] =b.y + (j + 1) * vectorABDACD.y / (i + 1); //точки на прямых между точками на AB и AC
}
k++;
}
}
int numbDotTEMP = numbDot;
NewX[numbDot] = a.x;
NewY[numbDot] = a.y;
newT[numbRect][0] = numbDot;
numbDot++;
NewX[numbDot] = ABDX[0];
NewY[numbDot] = ABDY[0];
newT[numbRect][1] = numbDot;
numbDot++;
NewX[numbDot] = ACDX[0];
NewY[numbDot] = ACDY[0];
newT[numbRect][2] = numbDot;
numbDot++;
numbRect++;
k = 0;
for (int i = 1; i < q; i++) {
if (i != q - 1) {
NewX[numbDot] = ABDX[i];
NewY[numbDot] = ABDY[i];
numbDot++;
}
else {
NewX[numbDot] = b.x;
NewY[numbDot] = b.y;
numbDot++;
}
for (int j = 0; j < i; j++) {
NewX[numbDot] = internal_points_X[k];
NewY[numbDot] = internal_points_Y[k];
k++;
numbDot++;
}
if (i != q - 1) {
NewX[numbDot] = ACDX[i];
NewY[numbDot] = ACDY[i];
numbDot++;
}
else {
NewX[numbDot] = c.x;
NewY[numbDot] = c.y;
numbDot++;
}
}
numbDotTEMP++;
for (int i = 0; i < q - 1; i++) {
for (int j = 0; j < 2 + i; j++) {
newT[numbRect][0] = numbDotTEMP;
newT[numbRect][1] = numbDotTEMP + 2 + i;
newT[numbRect][2] = numbDotTEMP + 3 + i;
cout << numbDotTEMP << "x=" << NewX[numbDotTEMP] << " y=" << NewY[numbDotTEMP]<< " " << numbDotTEMP + 2 + i<<"x=" << NewX[numbDotTEMP + 2 + i] << " y=" << NewY[numbDotTEMP + 2 + i] << " " << numbDotTEMP + 3 + i<< "x=" << NewX[numbDotTEMP + 3 + i] << " y=" << NewY[numbDotTEMP + 3 + i] << endl;
numbRect++;
if (j > 0) {
newT[numbRect][0] = numbDotTEMP - 1;
newT[numbRect][1] = numbDotTEMP;
newT[numbRect][2] = numbDotTEMP + 2 + i;
cout << numbDotTEMP-2 << "x=" << NewX[numbDotTEMP - 2] << " y=" << NewY[numbDotTEMP - 2] << " " << numbDotTEMP-1 << "x=" << NewX[numbDotTEMP - 1] << " y=" << NewY[numbDotTEMP - 1] << " " << numbDotTEMP + 1 + i << "x=" << NewX[numbDotTEMP + 1 + i] << " y=" << NewY[numbDotTEMP + 1 + i] << endl;
numbRect++;
}
numbDotTEMP++;
}
}
}
delete[] ACDX;
delete[] ABDX;
delete[] ACDY;
delete[] ABDY;
delete[] internal_points_X;
delete[] internal_points_Y;
for (int i = 0; i < size_T; i++) {
delete[] T[i];
}
delete[] T;
delete[] X;
delete[] Y;
T = newT;
X = NewX;
Y = NewY;
}
double Fuct(double x, double y) {
return 0;
}
void borderline(int a, int b, int c, double* X, double* Y, int q,function<double(double,double)> Fu,double* NewX, double* NewY, int** newT) {
cout << "a.x=" << X[a] << "a.y=" << Y[a] << endl;
cout << "b.x=" << X[b] << "b.y=" << Y[b] << endl;
cout << "c.x=" << X[c] << "c.y=" << Y[c] << endl;
double* CAX = new double[q + 1];
double* CAY = new double[q + 1];
CAX[0] = X[c];
CAY[0] = Y[c];
CAX[q] = X[a];
CAY[q] = Y[a];
Point vector;
vector.x = X[a] - X[c];
vector.y = Y[a] - Y[c];
for (int i = 1; i < q; i++) {
CAX[i] = CAX[0] + i * vector.x / q;
CAY[i] = CAY[0] + i * vector.y / q;
}
Point direction_vector;
direction_vector.x = X[b] - X[c];
direction_vector.y = Y[b] - Y[c];
double* r = new double[q + 1];
for (int i = 0; i < q + 1; i++) {
if (Fu(CAX[i], CAY[i]) == 0) {
r[i] = 0;
}
else {
//ЧМ
double x0 = 1000;
double x1 = 0;
double eps = 0.01;
double rez = x1, f0, f;
int iter = 0;
do {
f = Fu(CAX[i] + rez * direction_vector.x, CAY[i] + rez * direction_vector.y);
f0 = Fu(CAX[i] + x0 * direction_vector.x, CAY[i] + x0 * direction_vector.y);
rez = rez - f / (f - f0) * (rez - x0);
iter++;
}
while (fabs(f) > eps && iter < 20000);
r[i] = rez;
}
}
for (int i = 0; i < q + 1; i++) {
cout << "r" << i << "="<<r[i]<<endl;
}
NewX[0] = CAX[q] + r[q] * direction_vector.x;
NewY[0] = CAY[q] + r[q] * direction_vector.y;
int k = 1;
for (int i = 1; i < q+1; i++) {
for (int j = 0; j < i; j++) {
NewX[k] = CAX[q-i] + r[q-i] * direction_vector.x*j/i;
NewY[k] = CAY[q-i] + r[q-i] * direction_vector.y*j/i;
k++;
}
NewX[k] = CAX[q - i] + r[q - i] * direction_vector.x ;
NewY[k] = CAY[q - i] + r[q - i] * direction_vector.y ;
k++;
}
newT[0][0] = 0;
newT[0][1] = 1;
newT[0][2] = 2;
int numbDotTEMP=1;
int numbRect = 1;
for (int i = 0; i < q - 1; i++) {
for (int j = 0; j < 2 + i; j++) {
newT[numbRect][0] = numbDotTEMP;
newT[numbRect][1] = numbDotTEMP + 2 + i;
newT[numbRect][2] = numbDotTEMP + 3 + i;
cout << numbDotTEMP << " x=" << NewX[numbDotTEMP] << " y=" << NewY[numbDotTEMP] << " " << numbDotTEMP + 2 + i << " x=" << NewX[numbDotTEMP + 2 + i] << " y=" << NewY[numbDotTEMP + 2 + i] << " " << numbDotTEMP + 3 + i << " x=" << NewX[numbDotTEMP + 3 + i] << " y=" << NewY[numbDotTEMP + 3 + i] << endl;
numbRect++;
if (j > 0) {
newT[numbRect][0] = numbDotTEMP-1 ;
newT[numbRect][1] = numbDotTEMP;
newT[numbRect][2] = numbDotTEMP + 2 + i;
cout << numbDotTEMP - 2 << " x=" << NewX[numbDotTEMP - 2] << " y=" << NewY[numbDotTEMP - 2] << " " << numbDotTEMP - 1 << " x=" << NewX[numbDotTEMP - 1] << " y=" << NewY[numbDotTEMP - 1] << " " << numbDotTEMP + 1 + i << " x=" << NewX[numbDotTEMP + 1 + i] << " y=" << NewY[numbDotTEMP + 1 + i] << endl;
numbRect++;
}
numbDotTEMP++;
}
}
cout << " fsd fsd ";
cout << "a.x=" << NewX[0] << "a.y=" << NewY[0]<<endl;
cout << "b.x=" << NewX[6] << "b.y=" << NewY[6] << endl;
cout << "c.x=" << NewX[9] << "c.y=" << NewY[9] << endl;
for (int i = 0; i < 10; i++) {
cout << NewX[i]<<" "<< NewY[i]<<endl;
}
}
int main()
{
double* On = new double[n + 1];
for (int i = 0; i <= n; i++) {
On[i] = a + i * (b - a) / n;
}
double* r = new double[m + 1];
for (int i = 0; i <= m; i++) {
r[i] = (double)i / m;
}
pair<double, double>** B = new pair<double, double> *[n + 1];
for (int i = 0; i < n + 1; i++) {
B[i] = new pair<double, double>[m + 1];
}
for (int i = 0; i < n + 1; i++) {
for (int j = 0; j < m + 1; j++) {
B[i][j].first = Gr(On[i], r[j]) * cos(On[i]);
B[i][j].second = Gr(On[i], r[j]) * sin(On[i]);
cout << "number" << i << "-" << j << " " << "x=" << B[i][j].first << " y=" << B[i][j].second << endl;
}
}
if (b == 2 * pi) {
double* X = new double[n * (m + 1)];
double* Y = new double[n * (m + 1)];
for (int i = 0; i < n; i++) {
for (int j = 0; j < m + 1; j++) {
X[((m + 1) * i + j)] = B[i][j].first;
Y[((m + 1) * i + j)] = B[i][j].second;
}
}
int p = 2 * n * m;
int** T = new int* [p];
for (int i = 0; i < p; i++) {
T[i] = new int[3];
}
int k = 0;
for (int i = 0; i <= n - 2; i++) {
for (int j = 0; j <= m - 1; j++) {
T[k][0] = (m + 1) * i + j;
T[k][1] = (m + 1) * (i + 1) + j;
T[k][2] = (m + 1) * (i + 1) + j + 1;
k++;
T[k][0] = (m + 1) * i + j;
T[k][1] = (m + 1) * (i + 1) + j + 1;
T[k][2] = (m + 1) * (i)+j + 1;
k++;
}
}
int i = n - 1;
for (int j = 0; j <= m - 1; j++) {
T[k][0] = (m + 1) * i + j;
T[k][1] = j;
T[k][2] = j + 1;
k++;
T[k][0] = (m + 1) * i + j;
T[k][1] = j + 1;
T[k][2] = (m + 1) * (i)+j + 1;
k++;
}
int q = 3;
double* NewX = new double[(q + 1) * (q + 2) / 2];
double* NewY = new double[(q + 1) * (q + 2) / 2];
int** newT = new int* [q * q];
for (int i = 0; i < q * q; i++) {
newT[i] = new int[3];
}
function<double(double,double)> f = Fuct;
Not_borderline(T, 2 * n * m, X, Y,3);
savetostl(X, Y, T,2*n*m*q);
}
else {
double* X = new double[(n + 1) * (m + 1)];
double* Y = new double[(n + 1) * (m + 1)];
for (int i = 0; i < n + 1; i++) {
for (int j = 0; j < m + 1; j++) {
X[((m + 1) * i + j)] = B[i][j].first;
Y[((m + 1) * i + j)] = B[i][j].second;
}
}
int p = 2 * n * m;
int** T = new int* [p];
for (int i = 0; i < p; i++) {
T[i] = new int[3];
}
int k = 0;
for (int i = 0; i <= n - 1; i++) {
for (int j = 0; j <= m - 1; j++) {
T[k][0] = (m + 1) * i + j;
T[k][1] = (m + 1) * (i + 1) + j;
T[k][2] = (m + 1) * (i + 1) + j + 1;
k++;
T[k][0] = (m + 1) * i + j;
T[k][1] = (m + 1) * (i + 1) + j + 1;
T[k][2] = (m + 1) * (i)+j + 1;
k++;
}
}
Not_borderline(T, 2 * n * m, X, Y, n * (m + 1));
savetostl(X, Y, T,2*n*m);
}
}