Всем привет! Решал олимпиадные задачки, вот наткнулся на одну и второй день решить её не могу. Задача такая:
Решение в лоб тут не прокатит(перебрать все элементы массива с ai).
Когда я вспомнил про корневую декомпозицию то подумал, ну вот оно. Но пока писал код осознал что не понимаю как её тут применить. Накиньте мыслей по задаче пожалуйста, если они появятся:)
Допустим, что поступила команда типа 1 i. В ней просят найти элемент, больший по значению, чем ai.
Однако само это i может быть = |A|. |A| ≡ n, т.е. если ai это последний элемент массива, то никакое aj не подойдёт под два условия, которые в задании соединены союзом “и”, потому что никакое j не сможет быть j > i. Что надо выводить в качестве результата команды первого типа в этом случае?
На этот случай в описании формата сказано, что a|A| это самое большое число в массиве, которое точно больше всех остальных элементов по значению, и
i ≤ n - 1 в команде по условию, то есть про последний элемент гарантированно никогда не спросят.
ПОЭТОМУ он, этот последний элемент, всегда сможет быть ответом (больше любого элемента, и находится правее любого элемента).
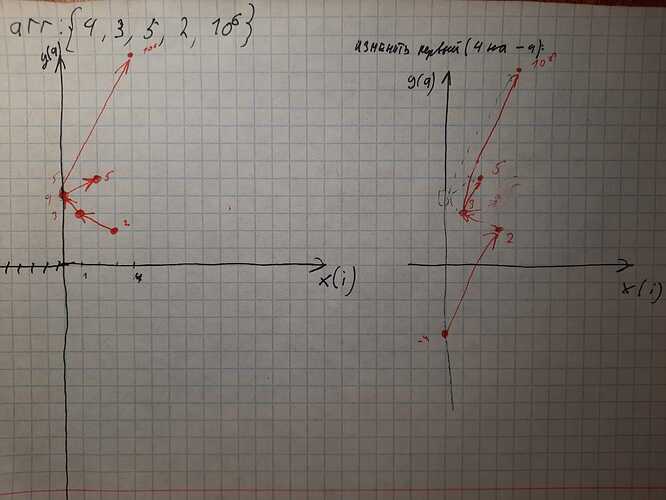
Нарисуем на координатной плоскости направленный ациклический граф, в котором вершины - это элементы входного массива (с координатами <x=i, y=ai>), а направленные рёбра изображают отношение “больше по значению и правее по индексу”.
Мы можем хранить не все рёбра, если ребро может быть заменено цепочкой других рёбер, то его хранить не надо.
Можно ещё хранить второй комплект рёбер в другую сторону (“меньше по значению и левее по индексу”).
Ребер из вершины будет несколько, но самые интересные - четыре.
Если смотреть по оси индексов, то ближайший самый высокий из узлов слева и самый низкий из узлов справа. А если смотреть вдоль оси значений, то самый левый из высоких и самый правый из низких.
Когда меняем знак, из графа вершину удаляем, добавляем в новое место.
Когда изымать будем, то можно будет по горизонтали соединить предыдущий узел со следующим. А когда будем вставлять - надо подумать. вероятно в месте вставки узлы будут соединены, потому что они соседние по значениям, эту связь надо будет разорвать и провести через вставляемый узел.
Сложность операции типа 2 = O(log2(n)), потому что это операция вставки в сортированный список + несколько O(1) для изменения связей.
Сложность операции типа 1 = O(1).
Сложность предварительного построения - надо посчитать, но кажется примерно как у сортировки O(4·n·log2(n)) или n2.
Если уже рассматриваем прямоугольник < <1;-105>,<n-1,105>>, то
можно делить на подпрямоугольники его, там вычислять для подпрямоугольников
минимальные, максимальные, левейшие и правейшие значения.
Вот это будет в духе корневой декомпозиции.
Надо сделать программы:
(Возможно, после просмотра нескольких случайных примеров и их результатов обработки прийдут какие-то новые мысли.)
Дальше пока мысль не идёт.
Держи в курсе. Мы волнуемся.
Естественно последний элемент в массиве больше любого другого, НО он будет ответом только в том случае, если не найдётся другого элемента, расположенного правее ai, и при этом большего чем ai. Т.к. в условии требуется найти наименьший элемент из всех подходящих…
Не очень понял что обозначает эта запись, буду рад если поясните
координаты - это упорядоченная пара <x, y>, состоящая из скаляров x и y, где x равно i, y = ai
Мне кажется я почти разобрался в Вашей мысли.
Но даже если понять как быстро вставлять и извлекать вершины, то мне пока совсем не очевидно как такую структуру данных хранить и ничего в голову не приходит(
как такую структуру данных хранить
Это направленный граф. Способы хранения графов - например списки вершин, списки рёбер (ещё есть “матрицей смежности”, но тут оно не надо).
Как раз оно то в голову и пришло, но безрезультатно
Но ведь нам ещё надо будет хранить i(x) и значение ai(y)
И в таком случае разве можно использовать списки вершин?
А в этом случае для каждой вершины нужно будет получается хранить много чего. Если абстрактно то так:?
ai: {x, y, [“множество с вершинами, в которые идут ребра из ai”]}
Напиши сначала несколько примеров, которые не будут решать задачу, но будут реализовывать какие-то близкие действия (выше я перечислял - ввод, вывод, сверки, хранение в памяти, возможно рисование).
