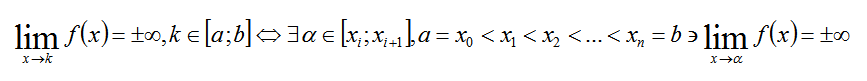Так там просто словесный понос сознания, неупакованный в русский язык, очевидно же 
Где? На комиксе про «Хотел писать игры»? По-моему, речь препода вполне нормальна. Другое дело, что там, судя по его речи, идёт лекция по матанализу, а на доске — записи, характерные для математической логики (булевой алгебры).
Она не нормальна, о чем говорит бесконечное повторение одних и тех же слов.
Речь требует местоимений и большего словарного запаса. Раз нет местоимений, значит, человек не удерживает в памяти контекст, что и называется “понесло”. Если контекст только в зрительной памяти, речь частенько тоже просто “несет” поверх.
На доску я не смотрел принципиально - качество шрифта ниже уровня человеческого достоинства  Возможно, так и задумано - текст отдельно, слова - отдельно. Рассинхрон.
Возможно, так и задумано - текст отдельно, слова - отдельно. Рассинхрон.
Нормальные и вполне логичные там слова для матанализа.
Слова нормальные, поток - нет.
“Если функция не ограничена на отрезке, то и хотя бы на одном из его участков” - вот это что-то около нормального русского языка.
язык математических доказательств и нормальный русский не одно и то же. И вообще его нормальность для сантехника и математика совершенно разная. Хотя бы на одном из его участков и для любого разбиения существует хотя бы один участок далеко не одно и то же
Там как раз попытка натянуть сову на глобус. Пока у вас формулы - никаких претензий и быть не может. Но там же даже не попытка чтения формул. Там именно попытка рассуждения русским языком.
Это одно и тоже. В языке всегда присутствует кванторизация. А вот течения времени в данном случае быть не должно. Если смущает “участок”, можно сказать “подотрезок”, но именно первое норма для русского языка. Вместо подмножеств, подпространств и т.п.
- [Допустим] (= если), функция не ограничена на отрезке, [тогда] (= то)
для любого [разбиения данного отрезка] (=его разбиения), [функция] (= она) [будет](убирается с мусорным течением времени) неограничена хотя бы на одном из [отрезков, полученных после разбиения] (= его участков). - Если функция не ограничена на отрезке, то [для любого его разбиения](убирается, т.к. участок подразумевает разбиение, которое по умолчанию любое) [она неограничена] (= и) хотя бы на одном из его участков.
Что-то матана много я расписал  , придется отрезать куда-то.
, придется отрезать куда-то.
По какому умолчанию? Математика строгая наука и любое умолчание специально оговаривается )
По умолчанию из определения свободной переменной) Пока не наложено ограничений, она - любая.
Если смущает сложная кванторизация русского языка, то можно вместо “для любого <отглагольного существительного>” обычно “как ни <глагол>”. Как ни лечи, как ни учи, как ни строй и т.п. Но они избыточны по своему смыслу, играют усилительную роль и поэтому склоняются к значению “в любом случае”. Отсюда “как ни крути”.
Тогда будет:
“…то и хотя бы на одном его участке, как ни дели”.
О, еще предлог с заменой падежа ушел)
И можно подумать, равносильны ли “хотя бы на одном” и “на каком-то” в данном случае. Скорее всего.
Производство лекции будет стоить дорого. Логических усилий на обработку русского уйдет больше, чем на матан)
После такой лекции не один студент сбежит, а все разбегутся… 
Я, если честно, так и не поняла, к чему претензия. Да, обычная человеческая речь не такая. И даже не такая, как я сейчас пишу. Но там тупо отрывок какого-то объяснения из учебника.
Да-да, таким вот дебильным языком, я помню, были написаны наши учебники. И такими же заученными оттуда фразами мы решали задачи по матану. Собственно, такими же словами в такой же стилистике бросалась и наша преподша, когда показывала пример решения. Разумеется, никто не перефразировал в нормальную речь то, что давалось в учебниках. Типа “а зачем, пусть голову поломают”.
Есть такие авторы, которые специально так пишут. Наверное, они думают, что если напишут попроще, то все станут считать их не слишком умными. Терпеть не могу таких авторов.
Не пойму…
При чем здесь речь и стиль мышления преподавателя?
Суть, изюминка комикса совершенно иная…
P. S.
ИМХО. Со стороны преподавателя довольно доступно изложено. В отличии от индивидуальной интерпретации того-же:
Вот здесь, точно ни фика не понятно… 
Больше скажу…
Не понятней чем здесь:
Суть комикса понятна.
Но разговор-то зашел про то, что именно говорит преподаватель.
Может потому что обсуждалась вырванная из контекста одна единственная деталь - квантор “для любого”…
Предложение полностью:
“Если функция не ограничена на отрезке, то и на каком-то его участке[, как ни дели]”.
Думаю, все гораздо проще - копипаста и распил бабла. А за посещение лекций начисляются баллы 
Тогда, когда мне нужны были учебники по матану что-то не встречал написанных в стиле, что предлагает MihalNik. Почему интересно? В основном это конечно Кудрявцев и Фихтенгольц. Можно еще вспомнить матан от Грауэрта, Либа и Фишера. Никольского еще помню. Все изданий 70-ых и 80-ых. Ага, распил бабла ))
Верно в те года не пилили. Т. к. только за мысль рапила реально ехали пилить лес, лет на 15…
Это типа в современных вузах набираешь балы только за то что присутствовал на лекциях? А слушал или втыкал в смартфон уже и не важно?
Так это верный путь к деградации…
Речь же не про тех авторов полувековой давности, а про то, что читают и пишут сейчас. А честные преподы, принимая экзамен, требовали “своими словами” для хорошей оценки. Потому что как раз не понимая смысла, это не получится сделать.
Строгость формулировок, которая в образовании с подачи Колмогорова - неоднозначная штука и политическое решение.
А долгое время до этого матан вообще с русским не скрещивали)
Я уже ответил - дорого очень. Потому что человек сможет изготовить значительно меньше. И обучать его для этого надо намного дольше. Копипаста же бесплатна по сути, можно изготавливать много - платят именно за объем, за кол-во публикаций и цитирований)
Давно уже. Иначе бы ни одного студента там не было)
Как по мне лучший учебник по дифференциальному анализу. В.Н. Худенко
https://old.kantiana.ru/mathematics/umk/
Вот с НС я бился очень долго бился что-бы разобраться как они работают хотя им уже пол-век но везде копируют одни и тежи формулы с ошибками по которым нельзя воспроизвести алгоритм. Слава богу в последнее десятилетие время общество с НС разобралось. Но и то мне пришлось собрать 10 статей скачать которые в сумме дают полное описание.
Я тут 3-тий день пытаюсь понять алгоритм, как привести матрицу к 3-х диагональному виду. На самом деле это уже второй подход к 5 учебникам добавил ещё 5 учеников. Так вот все учебники написаны в стиле, как в комиксе. Один хуже другого.
Вот из этого описания кто-то может догадаться откуда в матричном умножение взялось вычитание?
И почему матрицу L вычисляют через её саму же! Окак.
LDLT я разобрался. Вот только это мене не приблизило к разгадки алгоритма диагонализации.