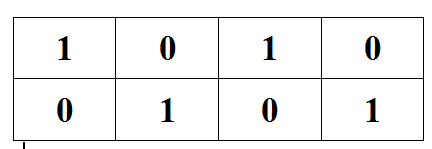СТАТЬЯ: Построение таблицы истинности (двоичных наборов) двумя способами

Научный форум Дискретная математика и математическая логика
#1

Построение таблицы истинности двумя способами.

В этот статье будут показаны примеры заполнения таблиц истинности двоичными наборами без вычислений значений каких бы то ни было булевых функциях на них. Я предполагаю, что читатель уже знаком с сопутствующей терминологией и двоичной системой счисления (далее — 2СС), поэтому не буду прояснять эти термины и рассказывать о переводе чисел из одной системы счисления в другую.

Итак, перед тем, как построить таблицу истинности, следует определиться с количеством строк и столбцов в ней.

Количество столбцов будет равно количеству переменных функции плюс один столбец на значение функции на двоичных наборах.

Количество строк в таблице (количество двоичных наборов) будет вычисляться по формуле 2n, где n — количество переменных функции. Ещё одна дополнительная строка отводится на шапку таблицы, куда записываются имена переменных и имя вычисляемой функции (или её аналитическое выражение). То есть, можно сказать, общее количество строк таблицы с учётом шапки будет равно 2n + 1.

Рассмотрим пример. Пусть дана функция трёх переменных F(x, y, z) (n = 3). Начертим таблицу для этой функции, но пока не будем заполнять. Итак, общее количество строк будет равно 23 + 1 = 9, один из которых отводится на шапку. Количество столбцов таблицы будет равно количеству переменных (три переменные) да плюс ещё один на значения функции. Итого 4 столбца. Имеем такую таблицу:

1

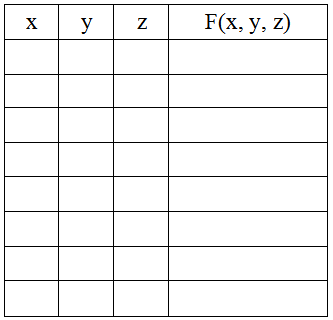
Первый способ («по горизонтали»).

Он основан на использовании 2СС. Полагаю, это стандартный способ, которым пользуются в большинстве случаев при решении задач, предполагающих использование таблиц истинности.

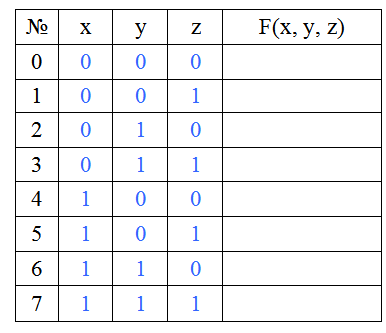
Для использования данного способа я рекомендую дополнять целевую таблицу истинности ещё одним столбцом слева. В нём мы будем нумеровать двоичные наборы, начиная с нуля (это важно). Таким образом, наша таблица истинности для трёх переменных принимает следующий вид:

2

Отступление. Почему надо нумеровать с нуля?

Есть, как минимум две причины, по которым это нужно делать:

  1. двоичные наборы нумеруются с нуля в условиях задач, решение которых предполагает работу с булевыми функциями и, в частности, работу с таблицами истинности. Например, вам может быть поставлена задача, найти МДНФ функции, заданной двоичными наборами, например, 0, 2, 6, 8, 15. Или, наоборот, найти номера двоичных наборов, на которых функция принимает значение «0». Если вы будете нумеровать наборы с единицы, то вы неверно решите задачи или не сможете решить их вообще;
  2. если вас интересует эта статья, то, скорей всего, вы изучаете дискретную математику или булеву алгебру. А из этого следует, что вы, возможно, обучаетесь на специальности/факультете, где параллельно изучаются дисциплины, связанные с программированием. В языках программирования сущности, являющиеся элементами коллекций или структур хранения данных (массивов, списков и так далее) также нумеруются с нуля. Я понимаю, что, если вы изучали язык Turbo Pascal, то, возможно вас учили определять массивы, нумерация элементов в которых начинается с единицы, а также, возможно, вы сталкивались с таким типом данных, как строки в этом же языке, где нумерация символов также начинается с единицы. Тем не менее, ввиду вышесказанного, вам следует привыкнуть к нумерации элементов с нуля.

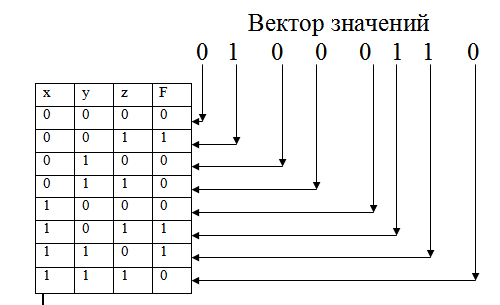
Теперь, чтобы вам было легче понимать этот способ, вспомните телевизионное шоу «Поле чудес». Там каждая буква слова записывалась в отдельной клетке. Здесь мы будем поступать так же. Только записывать мы будем не слова, а двоичные числа. Эти числа мы получим путём перевода номеров двоичных наборов из десятичной системы счисления в двоичную. Например, возьмём набор с номером 3. Переведём тройку в 2СС и получим 112. Нам надо заполнить три клетки, но полученное число состоит только из двух цифр. Чтобы данное число не изменилось, в оставшиеся пустые клетки мы можем записать только нули. Поэтому правило дополнения любого двоичного набора такое: все пустые клетки (они будут располагаться слева от заполненных клеток) заполняются нулями. После выполнения этой операции над всеми оставшимися номерами наборов мы получим следующую картину:

3

Чтобы закрепить полученные знания, попробуйте самостоятельно построить таблицу истинности для функции от пяти переменных: f(a, b, c, d, e)

Второй способ («по вертикали»).

В этом способе вам не потребуется дополнять таблицу столбцом с номерами двоичных наборов и переводить их в 2СС.

Чтобы понять суть метода, давайте у заполненной таблицы в двоичных наборах раскрасим нули синим цветом, а единицы — красным. Получим:

4

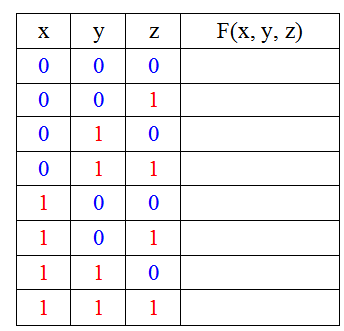
Посмотрите на столбцы. Можно заметить, что непрерывные серии из нулей/единиц чередуются, при этом длина серии (количество элементов, её составляющих) увеличивается в два раза при движении влево на каждой позиции и, наоборот, уменьшается в два раза при перемещении вправо на каждой позиции. Так, длина серии в столбце, соответствующем первой переменной (x) — максимальна и равна 4, а для последней переменной (z) — минимальна и равна 1.

В общем случае, длина серии в столбце, соответствующем первой переменной будет равна 2n / 2 = 2n-1, где n — количество переменных функции. При смещении вправо длину серии следует сокращать вдвое на каждой следующей позиции. На столбце для последней переменной длина серии окажется равной 1.

Вот вторая вариация метода. Если двигаться в обратном направлении и с другого конца (крайний правый столбец для последней переменной функции), то длинна серии в начале будет равна 1, а при движении влево её длина будет удваиваться на каждом следующем столбце, достигнув в итоге значения 2n-1 на крайнем левом столбце.

Я считаю, что преимущество такого способа состоит в быстроте заполнения. Например, все таблицы с двоичными наборами, которые были приведены в данной статье, были заполнены именно этим методом, при этом я начинал заполнение с крайнего левого столбца.

Попробуйте попрактиковаться, заполнив таблицу этим способом, решив пример для самостоятельной работы из описания предыдущего способа.

Отступление. Можно ли менять порядок двоичных наборов?

Нет, нельзя. Даже если вы верно вычислите значения функции на всех наборах, вектор значений функции у вас будет соответствовать другой функции, отличной от той, над которой вы работали. В некоторых задачах от вас может потребоваться записать вектор функции в качестве ответа. Если вы измените порядок двоичных наборов и выпишите вектор значений то получите неверный ответ и задачу вам не засчитают.


P. S. Примеры для самостоятельной работы предназначены, разумеется, для тех, кто интересуется материалом в целях обучения, а не для всех вообще, кто читает эту тему. Пусть каждый для себя сам решает, будет он решать примеры из этой статьи или нет. Материал предназначен главным образом для тех, кто хочет научиться строить и заполнять таблицы истинности.

#2

Мамочки… Я 16 лет знаю про таблицы истинности, и то поняла, что ты хочешь сказать лишь со второго раза. Как-то слишком сложно.

Что значит “вектор функции” и “вектор значения”? Приведи пример задачи, где нельзя менять порядок двоичных наборов.

#3

Банально, но очень замысловато написано )). Заголовок статьи не корректный.

Тут не описано как строить таблицу истинности, а записано как сформировать в виде таблицы наборы входных данных для функции из N двоичных аргументов.

Из википедии: Таблица истинности — таблица, описывающая логическую функцию.

(в общем случае функция может выполняться не только над двоичными числами).

Пример таблицы построенный в онлайн калькуляторе:

Снимок экрана от 2020-01-24 14-01-37
Снимок экрана от 2020-01-24 14-01-37952×338 123 KB

Ну а вы тут описали как заполнить первые 3 столбца.

Но это все тоже банально. Вот что интересно. Зачем хранить таблицу истинности в памяти? - чтобы не вычислять повторно значение функции. Это единственное назначение, т.е. что-то типа Таблиц Брадиса - вообще это техника оптимизации программ, известная с древности, она же мемоизация или табулирование. И если мне пришлось решать эту проблему, значит:

  1. я пишу какой-то специфический математический софт;
  2. этот софт большой и медленно работает (иначе мне не пришлось бы заниматься оптимизацией кода и я вычислял бы функцию каждый раз заново).
  3. Тормозит он скорее всего потому, что функции долго вычисляются, а значит, скорее всего они от большого числа аргументов.

Ну а если так, то хранение таблицы в памяти должно быть оптимальным. Вот про это можно было бы написать. Ну потому что хранить все эти наборы, которые вы сформировали (000, 001, 010, …) - это ужасно. Ведь если у меня функция от 20 аргументов (а это не предел в большом математическом софте), то каждый набор сордержит 20 чисел, а всего таких наборов 1048576. Итого, нужно хранить 20971520 чисел, представляющих собой аргументы функции.

Первый вариант (курильшика)- это хранение всех этих наборов в памяти. Вот только тогда для заполнения можно использовать ваш “второй метод”. Правда профита я с него никакого не вижу. Вычислительнная сложность такого метода никак не может быть ниже (N^2)*N. Где N - количество аргументов функции. А это фантастически высокая асимптотика.

Единственное над чем тут есть смысл думать - оптимальная упаковпа этих данных в памяти, ну потому что числа то все бинарные, а как мы знаем - компьютер адресует память байтами. То есть нужно сгородить что-то типа специализации шаблона vector, а мы знаем что это больное место в С++.

Проблема при таком подходе у нас во всем. Хотим мы вычислить f(1,0,1,0,0,0,0,0,1,1,1,0,1,1). Как найти в таблице нужное значение? - Ну вы ведь для того чтобы оптимизировать строили таблицу, а не просто “по фану”? - Если вы планируете для искать в таблице нужное значение линейным поиском - то ваша производительность просядет в (N^2)*N раз - ведь именно столько строк таблицы вы будете перебирать в худшем случае.

Собственно отсюда приходит второй вариант (здорового человека). Вообще не хранить эти наборы, а хранить вектор типа
bool array[n];
Элемент массива - хранит значение функции. Аргумент (вот эти 000, 001, 010) - это индекс элемента.

при вычислении f(1,0,1,0,0,0,0,0,1,1,1,0,1,1) быстренько (за O(N)) преобразуем аргумент в десятичное число, задающее индекс и получаем нужный нам элемент массива.

При заполнении таблицы - используем тот же индекс, меняем его значение от 0 до 2^N и каждый раз преобразуем его двоичное число.

Самое главное, что при таком подходе никому нафиг не нужны отдельно все значения десятого аргумента функции.

А что еще можно сделать? -

  1. вместо массива использовать дек, построенный на векторах, ну потому что цельного куска памяти для хранения 2^N значений может и не найтись.

  2. смастерить хороший тип данных для представления аргумента функции. Ну потому что реально, для функций с большим число аргументов массив не сойдет - ведь 2^N растет очень быстро.

  3. раз массив не сойдет - смастерить хорошую структуру данных для хранения таблицы истинности (скорее всего, основанную на деках из пункта 1).

1 лайк
#4

О, я тоже много лет знаю основы этого, и показалось странным, что тут какие-то 0, 1 и F вместо чего-то простого и понятного типа

A B A and B
0 0 0
1 0 0
0 1 0
1 1 1

:upside_down_face:

#5

Эти два термина означают одно и то же. Полностью он звучит так: «Вектор значений функции». Просто разница в написании продиктована лишь тем, что пропущены разные слова в исходном термине.

А означает этот термин значения функции, выписанные из столбца значений функции, начиная с верхней строчки. Например, возьмём простую функцию — дизъюнкцию. Имеем такую таблицу:

A B A V B
0 0 0
0 1 1
1 0 1
1 1 1


кстати, почему здесь нельзя прорисовать границу у HTML-таблицы, непонятно

Посмотрим на столбец значений функции. Выпишем сверху вниз значения и получим: 0111. Это и есть вектор значения функции.

Если мы поменяем двоичные наборы местами в этой таблице и вычислим функцию на них, то получим

A B A V B
1 1 1
0 1 1
1 0 1
0 0 0

Выпишем вектор (1110) и посмотрим на него в отрыве от нашей таблицы истинности. Вектор функции — это один из способов задания булевой функции. Если вставить этот вектор в таблицу с нормально расположенными наборами (а именно из таких таблиц выписываются вектора значений), то мы увидим, что у нас получилась другая функция, а именно И-НЕ (она же функция/штрих Шеффера, обозначается A | B).

Отсюда следует, что наборы менять нельзя ни в каком случае. Я понимаю, что можно выписать вектор функции в верном порядке (в порядке возрастания номеров двоичных наборов), но нам всё равно надо выполнять лишнюю работу. Лучше потратить эти силы на запись наборов в верном порядке, чем более, что это знающего человека это несложно.

Я бы не говорил о неверном порядке следования двоичных наборов, если сам лично это не увидел в работе своего заказчика (кому задачу фрилансил).

Аналитическое выражение может быть очень длинным. Гораздо проще где-то до таблицы записать, что f(x1, x2, …, xn) = <офигенно длинное выражение>, а уже в таблице писать f.

#6

@rrrfer вам позже отвечу

#7

Наверно в CSS убраны рамки, так модно сейчас ) https://www.darkhorseanalytics.com/blog/clear-off-the-table
Ну а в пост CSS вставить понятно нельзя, тогда б можно было менять почти что угодно на всей странице.

Так что проще мд https://www.tablesgenerator.com/markdown_tables

1 лайк
#8

Это я приблизительно и поняла из контекста вчерашнего сообщения. Больше интересует именно смысл этого вектора. Зачем его может понадобиться вычислять? И что это за таблица векторов? Она зачем нужна и где применяется? Пока что это больше похоже на “мы находим трудности и мужественно их преодолеваем”.

Что за задача у заказчика была-то?

#9

Бывают типы-множества, которые сразу так скрывают поразрядные операции - и код короче, т.к. нули опускаются, и в тоже время названия единиц понятные.

#10

Если честно, я не знаю, в чём конкретно его смысл. Вероятно, он может оказаться полезным тем, кто занимается цифровой электроникой, синтезирует схемы из простейших логических вентилей (И, ИЛИ, исключающее ИЛИ) и более сложных ([де]мультиплексоров, [де]шифраторов, триггеров). Когда изучал её в институте, там также было много работы с булевыми функциями и таблицами истинности. Но векторов у нас не было. Возможно, надо ещё больше погрузиться, чтобы возникла необходимость в работе с ними.

Однако, в защиту векторов функций могу сказать, что так очень удобно задавать функцию. В смысле, компактно. Это целесообразно, если, например, писать софт для работы с булевыми функциями. Вместо целой таблицы истинности нам надо просто хранить вектор значений.

Однако, есть ещё более компактный способ хранения. Хранить не вектор функции, а её номер. Он легко получается из вектора, так как последний является двоичным представлением её номер. Если мы запишем вектор, записанный сверху вниз, слева направо, то мы получим. номер функции, переведённый в двоичную СС.

Опять-таки, это нам может быть неясно зачем нужные вектора функций и их номера. Я не знаю, но полагаю, что эта информация очень полезна для инженеров-электронщиков, работающих с цифровыми компонентами. Думаю, они знают номера функций наизусть. Причём, чем больше аргументов у функции, тем больше существует функций в таким количеством аргументов. Количество функций от n аргументов вычисляется вычисляется как 2^2^n. Думаю, эти инженеры знают их все.

Я не употреблял такого термина. Что ты имеешь в виду?

Программистам могут задать аналогичный вопрос: для чего нужны все эти структуры хранения данных (стеки, деки, списки, деревья), когда можно обходится [статическими] массивами?

Вообще, там было несколько пунктов. Мне осталось доделать один: преобразовать заданную функцию к базису Пирса (стрелка Пирса, ИЛИ-НЕ).

@rrrfer
Не знаю, зачем вы это связываете с программированием. Да, статья банальная, но я хотел как-то помочь форуму (и студентам, изучающим ДМ) в этом плане. Я написал ровно столько, сколько им нужно для понимания материала. Ни о какой разработке речи пока не шло. Если бы я написал об этом, они бы запутались. Им бы сначала это усвоить. Это всё равно, что если бы я писал статью для школьников, в которой рассказывал как решать квадратные уравнения, а вы бы мне написали, что уравнения могут быть и не только квадратными, а намного сложнее, комбинированного вида, написав после чего, что лучше всего мне надо описывать методы для численного решения уравнений, некоторые из которых (метод Ньютона, например) требуют вычисления первой и второй производной в численном виде.

#11

Вот это:

Это совершенно разные структуры для совершенно разных целей. Например, глупо использовать список, когда тебе надо обращаться к структуре по индексу. И глупо использовать массив, когда у тебя идет постоянная вставка-удаление элементов - это проще сделать со списком. По дереву быстрее поиск элемента. Стек нужен, когда ты постоянно манипулируешь последним значением, а остальные не важны. Так что аналогия такая себе.

Что касается таблицы истинности, ну что мне с того, если я узнаю, что функция x & y ^ z || a & !b = 5678. Мне надо сначала перевести 5678 в двоичную систему. Допустим, я получу 10100, и что я буду с этими данными делать? Что мне это даст? (Значения в этом примере взяты с потолка, если что)

#12

Я не понимаю как это связано с дискретной математикой и как это может помочь студентам.
Почему я связал это с программированием? - потому что вы предложили АЛГОРИТМ заполнения таблицы значений фукнкции. Ну раз есть алгоритм, значит надо его реализовать? Один из вариантов реализации - программа.

Да и дискретная математика очень сильно связана с программированием. Все эти графы и конечные автоматы не для реализации в виде программ по вашему?

#13

Ну так они ответят, что это абстракции позволяющие разрабатывать программы проще и быстрее, делать их производительнее.

А внутри какие-то из них вполне могут реализованы и с помощью массива.

Списком могут называть и абстрактный тип данных https://en.wikipedia.org/wiki/List_(abstract_data_type), а не только связный список. Тогда он может быть реализован с помощью массива и иметь быстрый доступ по индексу.

#14

Я имел в виду, что ты возьмешь вектор значений функции и по одной компоненте будешь вписывать в каждую клетку столбца для значений функции, начиная с самой верхней. Вот нарисовал картинку (значения функции взяты с потолка):
2020-01-26_22-18-08

А что ты будешь делать, если тебе надо получить доступ к элементу списка с определённым номером? Да, у элементов списка нет индексов, но в качестве индекса можно использовать порядковый номер элемента. Тебе задали индекс, ты отсчитала с начала/конца списка нужный элемент и, например, вернула из функции.

Здесь, я думаю, так же можно ответить. Это совершенно разные способы заданий булевых функций.

Аналитический способ заданий функций удобен в том случае, когда, например, когда надо упростить функцию, не прибегая к построению таблицы истинности и минимизации посредством карт Карно. Более того, не все МДНФ/МКНФ являются самыми компактными по записями вариантами.

Мне в период моего обучения встретилась функция трёх переменных, которая на четырёх наборах принимала значение 1, а на остальных четырёх — 0. Причём, наборы относительно друг друга располагались таким образом, что, М(К/Д)НФ полученная с помощью карты Карно представляла бы собой либо четыре конъюнкции, либо столько же дизъюнкций. Одногруппники жаловались, что преподаватель не принимает такой ответ у них, так как он был не оптимальный. Я за эту задачу взялся позже остальных и у меня получилось с помощью равносильных преобразований добиться максимально компактной записи, пусть и не в базисе {И, ИЛИ, НЕ}, но такой задачи и не стояло.

Я говорю о дисциплине под названием «цифровая схемотехника». Нам надо было по заданной временной диаграмме построить оптимальную логическую функцию.

Карта Карно, полученная в этой задаче имела вид:
2020-01-26_22-50-34

Полученная в результате оптимизации функция имела такой вид:
a ^ b ^ c (^ — исключающее или).

А логическая схема была упрощена до одного трехвходового логического вентиля.

Задание функции таблицей истинности может быть удобно в технической документации на какие-то сложные логические элементы/компоненты.

Задание функции в виде двоичных наборов (или их номеров), где функция истинна может быть удобно для построения СДНФ (ну, или СКНФ) (что может быть использовано для синтеза схем в полном булевом базисе)

Вектором значений функция задаётся для компактности. Всё же хранить функцию в виде вектора намного удобнее и экономичнее, особенно если количество её переменных велико.

Прежде всего, скажу, что запись очень странная. Никогда такого не видел. Я не про значения, которые с потолка, это ладно. Я про то, что у тебя здесь, похоже, имеет место комбинация аналитического и номерного способа задания функции. Для чего нужно аналитическое задание функции, я писал выше, а о задании функции номером писал ещё выше:

Теперь, зачем всё это нужно.
Вообще, в программировании эти знания нужны, скорей всего, лишь для более глубокого понимая предметной области, если ты разрабатываешь какой-то софт для работы булевыми функциями, таблицами истинности и логическими схемами.

Напрямую эти знания будут нужны, думаю, инженерам электронщикам, которые синтезируют логические схемы, я об этом писал выше, в предыдущих постах.

#15

так там про скорость доступа речь.

С чего вдруг? Они есть и в связном списке, просто время доступа больше, поэтому связный список скорее всего не лучший выбор если надо часто это делать.

#16

Про скорость доступа согласен

Хранить индексы у списка, я так полагаю, нецелесообразно. На это требуется дополнительная память, кроме того, если ты удалишь какой-то элемент, тебе придётся пересчитать индексы. Я ведь верно понимаю?

#17

Так тут не про какое-то специальное индексирование речь, а про просто доступ по номеру, который возможен в любом списке, не важно как он внутри реализован (связный список, массив), вопрос только в скорости.

#18

ИМХО, с дискретной математикой это связано тем, что булева алгебра, а именно по этой дисциплине у меня написана статья, изучается в рамках курса дискретной математики. Во всяком случае, у меня в институте так и было.

Как это может помочь студентам? Разве у студентов не возникают вопросы по тем или иным моментам? Я лично сталкивался с тем, когда студентам было непонятно, как строить таблицу истинности. Один из них был моим заказчиком во фрилансе. Значит, спрос на информацию всё же есть. Почему бы мне не предоставить её, если у меня есть такая возможность?

По определению, алгоритм — строго упорядоченная последовательность действий, направленных на достижение какого-то результата. То есть, решение любой задачи предполагает использование алгоритма, даже такой простой, как, например, решение линейного уравнения.

Но, чтобы составить программу надо понимать, как это делать вручную. И эту статью я как раз написал, чтобы у студентов сформировалось понимание решения задачи. А имея знания, алгоритм всегда можно составить, как и написать программу.

И ещё один момент есть. Статья, повторюсь, ориентирована в том числе на студентов. Когда у них будет контрольная / зачёт / экзамен, их посадят в аудиторию без компьютеров, и знания о составлении программ в данном случае будут бесполезны.

Я даже больше скажу. Если они будут сдавать какую-нибудь дисциплину, предполагающую использование компьютера для написания программы, некоторые вещи им будет всё равно запрещено выполнять с помощью компьютера.

Например, когда мы сдавали вычислительную математику, то для численного решения уравнений нам было запрещено строить графики функций с помощью ПК, используя математические пакеты. Всё надо было делать на бумаге

График функции строился для того чтобы отделить приближения корней. Был задан отрезок, на котором надо было решить уравнение, а найденный нуль функции использовался как первое приближение.

Скажем так, их целесообразно использовать в алгоритмах программ, равно как и численные методы, потому что и то, и другое будет достаточно долго выполняться, если делать всё вручную.

#19

Если вы не решали конкретную задачу - то мне вообще не понятно к чему вот это все. Потому что, ЧТО, черт возьми, может быть проще чем перебрать 000 001, 010, 011, … ? Какие нафиг “методы”?

Если аргументов мало - то просто делаем так:

for (int i = 0; i < pow(2, n); ++i) {
  // все, таблица готова
}

Тут n - количество аргументов у твоей функции. Строка таблицы (00101) задается битами числа i. Ну если тебе не нравятся биты - перепакуй это в вектор (хотя я не уверен что это хорошо). Ну например вот:

    #include <iostream>
    #include <vector>
    #include <cmath>

    using namespace std;

    vector<bool> getArgs(size_t row, size_t nArgs) {
      vector<bool> args(nArgs);
      for (size_t i = 0; i < nArgs; ++i) {
        args[i] = row & 1;
        row = row >> 1;
      }
      return args;
    }

    bool foo(bool x, bool y, bool z) {
      return x ^ y & z;
    }

    int main () {
      size_t nArgs = 3;

      cout << "x y z f" << endl;
      for (size_t i = 0; i < pow(2, nArgs); ++i) {
        auto args = getArgs(i, nArgs);

        for (auto arg : args) {
          cout << arg << ' ';
        }
        cout << foo(args[0], args[1], args[2]) << endl;
      }
    }

Меньше 5 минут ушло у меня на написание этого кода. И он, черт возьми, выводит на экран таблицу истинности для трех аргументов и рассчитывает функцию для каждого из них.

Вот это очень странно. Потому что я не знаю зачем тогда эти студенты вообще учатся.