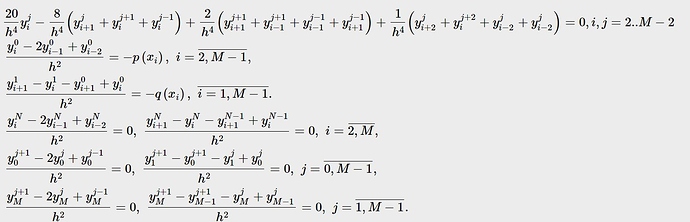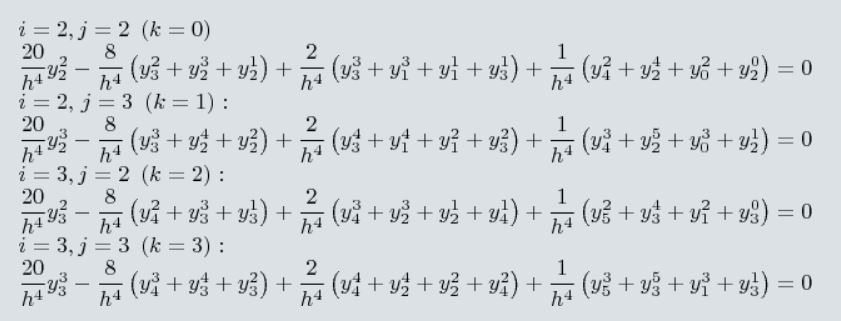Вам именно исходную механическую формулировку? Или математическую?
Если механическую, то у нас есть плоская задача теории упругости в полупространстве. На плоскость z = 0 действует нагрузка p(x) (она может быть либо постоянной, либо как-то зависящей от координаты x) – нагрузка действует на конечном отрезке. Нужно определить напряжения и деформации при действии такой нагрузки на полуплоскость. Ну поскольку значение напряжений на бесконечности не задашь при численной реализации, то мы с преподавателем решили рассмотреть прямоугольную область [-a,a]х[0,b], b достаточно большое, больше, чем ширина участка действия нагрузки. Постановка этой задачи есть в книге Джонсона по механике контактного взаимодействия (стр 21). Цель работы – исследовать напряженно деформированное состояние в случае различного вида нагрузок и ширины участка нагружения…
Дальше была получена математическая постановка задачи – краевая задача для бигармонического уравнения в прямоугольнике с условиями такого вида. Уравнение было получено из основных соотношений теории упругости (условия совместности деформаций, закона Гука и т.п.) Для удобства была введена функция Эри, через которую и выражается напряжение и деформации…
Дальше нужно решить это уравнение численно. Я выбрал с помощью метода конечных разностей – получить систему уравнений на значение сеточной функции y_i^j в каждой точке сетки. Разностная схема представлена выше. У меня возникла идея, что можно по системе уравнений получить матрицу коэффициентов перед неизвестными и дальше любыми методами получить решение системы. И возникла проблема (даже не проблема скорее всего, а затруднение) – как автоматически заполнить эту матрицу. Т.е., если я знаю двойную индексацию переменной, получить ее позицию в столбце матрицы A[k][m] – k-номер уравнения, m – номер столбца.
Я полагаю, что если я знаю , какая у меня переменная (точнее ее индексацию) y[i[j], то в каждой k строке ее позиция есть Mj + i + 1…
Поэтому я и спросил, как все таки явно получить эту зависимость, да даже проще говорять, по системе уравнений получить матрицу системы относительно y[0][0], y[1][0] , … y[M][N]. Если эту систему записать на бумажке в случае сетки из 25 точек…
Если у вас будут идеи по поводу того, как заполнить эту матрицу – буду очень рад! Просто уже долго сижу с этой проблемой и пока оптимального решения не нашел…
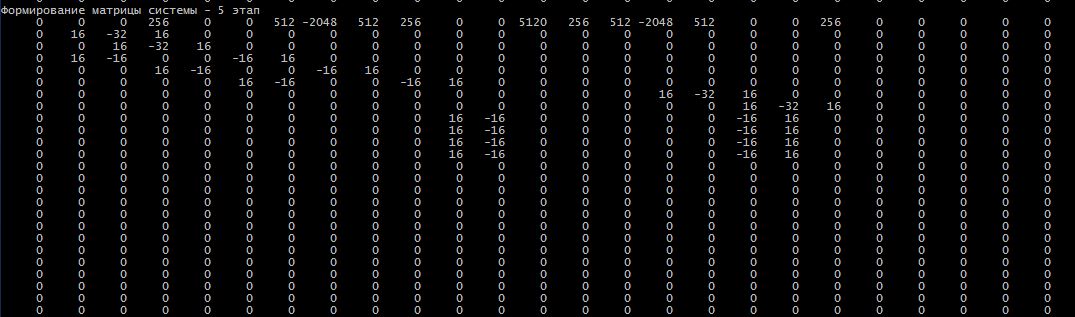
Ниже представил код своих попыток – в некоторых местах позиция коэффициентов совпадает… Но не везде…
cout << "Формирование матрицы системы - 1 этап" << endl;
for (int k = 0; k < (m - 3) * (n - 3) ; k++)
{
for (int i = 2; i <= (m - 2); i++)
{
for (int j = 2; j <= (n - 2); j++)
{
A[k][i + 1 + m * j+1] = 20 / pow(h_x, 4);
A[k][i + 2 + m * j + 1] = -8 / pow(h_x, 4);
A[k][i + 1 + m * (j + 1)] = -8 / pow(h_x, 4);
A[k][i + 1 + m * (j - 1)] = -8 / pow(h_x, 4);
A[k][i + 2 + m * (j+1)] = 2 / pow(h_x, 4);
A[k][i + m * (j+1)] = 2 / pow(h_x, 4);
A[k][i + m * (j-1)] = 2 / pow(h_x, 4);
A[k][i + 2 + m * (j-1)] = 2 / pow(h_x, 4);
A[k][i + 3 + m * j] = 1 / pow(h_x, 4);
A[k][i + 1 + m * (j + 2)] = 1 / pow(h_x, 4);
A[k][i - 1 + m * j] = 1 / pow(h_x, 4);
A[k][i + 1 + m * (j - 2)] = 1 / pow(h_x, 4);
}
}
}
out_of_system(A);
cout << "Формирование матрицы системы - 2 этап" << endl;
int q0 = 1;
int r0 = 2;
for (int k = (m - 3) * (n - 3); k < (m - 3) * (n - 3) + m - 2; k++)
{
B[k] = -p(X[k], a, selector);
A[k][r0 + 1 + q0] = 1 / pow(h_x, 2);
A[k][r0 + 1 - 1 + q0] = -2 / pow(h_x, 2);
A[k][r0 + 1 - 2 + q0 ] = 1 / pow(h_x, 2);
r0++;
}
out_of_system(A);
int q1 = 1;
int r1 = 1;
cout << "Формирование матрицы системы - 3 этап" << endl;
for (int k = (m - 3) * (n - 3) + m - 2; k < (m - 3) * (n - 3) + m - 2 + m - 1; k++)
{
A[k][r1 + 1 + m*0 + r1 * q1] = 1 / pow(h_x, 2);
A[k][r1+1 + 1 + m*0 + r1 * q1] = -1 / pow(h_x, 2);
A[k][r1 + 1 + m*1 + r1 * q1] = -1 / pow(h_x, 2);
A[k][r1 + 1 + 1 + m*1 + r1 * q1] = 1 / pow(h_x, 2);
r1++;
}
out_of_system(A);
int q2 = 1;
int r2 = 2;
cout << "Формирование матрицы системы - 4 этап" << endl;
for (int k = (m - 3) * (n - 3) + 2*m - 3 ; k < (m - 3) * (n - 3) + 3*m-5; k++)
{
A[k][r2-2 + 1 + n*n + r2*q2] = 1 / pow(h_x, 2);
A[k][r2-1 + 1 + n*n + r2*q2] = -2 / pow(h_x, 2);
A[k][r2 + 1 + n*n + r2*q2] = 1 / pow(h_x, 2);
r2++;
}
out_of_system(A);
int q3 = 1;
int r3 = 0;
cout << "Формирование матрицы системы - 5 этап" << endl;
for (int k = (m - 3) * (n - 3) + 3 * m - 5; k < (m - 3) * (n - 3) + 4 * m - 5; k++)
{
A[k][r3 + 1 + 1 + n*n + r3*q3] = 1 / pow(h_x, 2);
A[k][r3 + 1 + n*n + r3*q3] = -1 / pow(h_x, 2);
A[k][r3 + 1+ 1+ (n-1)*(n-1) + r3*q3] = -1 / pow(h_x, 2);
A[k][r3 +1 + (n-1)*(n-1) + r3*q3] = 1 / pow(h_x, 2);
}
out_of_system(A);
/*cout << "Формирование матрицы системы - 6 этап" << endl;
int q4 = 1;
int r4 = 0;
for (int k = (m - 3) * (n - 3) + 4 * m - 5; k < (m - 3) * (n - 3) + 4 * m - 5 + n-1; k++)
{
A[k][0 + (r4+1)*n + r4*q4] = 1 / pow(h_x, 2);
A[k][0 + r4 * n + r4 * q4] = -2 / pow(h_x, 2);
A[k][0 + (r4 - 1) * n + r4 * q4] = 1 / pow(h_x, 2);
}
int q5 = 1;
int r5 = 0;
for (int k = (m - 3) * (n - 3) + 4 * m - 5 + n - 1; k < (m - 3) * (n - 3) + 4 * m - 5 + 2*(n - 1); k++)
{
A[k][1 + (r5+1)*n + r5*q5] = 1 / pow(h_x, 2);
A[k][0 + (r5 + 1) * n + r5 * q5] = -1 / pow(h_x, 2);
A[k][1 + (r5 + 0) * n + r5 * q5] = -1 / pow(h_x, 2);
A[k][0 + (r5 + 0) * n + r5 * q5] = 1 / pow(h_x, 2);
}
int q6 = 1;
int r6 = 0;
for (int k = (m - 3) * (n - 3) + 4 * m - 5 + 2 * (n - 1); k < (m - 3) * (n - 3) + 4 * m - 5 + 3 * (n - 1); k++)
{
A[k][m + (r6 + 1) * n + r6 * q6] = 1 / pow(h_x, 2);
A[k][m + r6 * n + r6 * q6] = -2 / pow(h_x, 2);
A[k][m + (r6 - 1) * n + r6 * q6] = 1 / pow(h_x, 2);
}
int q7 = 1;
int r7 = 0;
for (int k = (m - 3) * (n - 3) + 4 * m - 5 + 3 * (n - 1); k < (m - 3) * (n - 3) + 4 * m - 5 + 4 * (n - 1); k++)
{
A[k][m + (r7 + 1) * n + r7 * q7] = 1 / pow(h_x, 2);
A[k][m-1 + (r7 + 1) * n + r7 * q7] = -1 / pow(h_x, 2);
A[k][m + (r7 + 0) * n + r7 * q7] = -1 / pow(h_x, 2);
A[k][m-1 + (r7 + 0) * n + r7 * q7] = 1 / pow(h_x, 2);
}